Want to accelerate your distance, angle, and dihedral calculations with blazing speed? You are in luck! As part of an MDAnalysis CSI EOSS project, Richard Gowers and I developed distopia, a high-performance Python library designed to efficiently compute these geometric measures under periodic boundary conditions (PBCs) using explicitly vectorised SIMD. Distopia is compatible with common PBC types, is highly performant on modern CPUs at single and double precision with minimal code changes, and is usable either as a standalone package or from within MDAnalysis’ distance backend. We think we have one of, if not the fastest package for calculating distances, angles and dihedrals under PBCs on a CPU but would love to be proved wrong!
Background
Molecular simulation workflows are often highly FLOP intensive, which has led to the development of high-performance compiled library layers alongside libraries written in higher level languages. MDAnalysis is one such library with a Cython/C++ auxiliary library for critical common operations alongside a Python core. These include operations like calculating distances, angles and dihedral angles under various periodic boundary conditions, such as orthorhombic and triclinic unit cells. These operations are often the base components on which other computations are built and as such are among the most critical to optimise.
While the switch to a compiled library layer results in significant speedups relative to unmodified code, we can do better! Compiled library layers are optimised for speed by the compiler, including with auto-vectorisation, where the compiler attempts to convert scalar code paths to vectorised SIMD enabled operations. However, as has been repeatedly documented, compilers are not all seeing and can often miss opportunities to vectorise code where large transformations are involved, leaving performance on the table.
Additional performance can be unlocked with hand written explicitly vectorised SIMD code. This is most often achieved using CPU intrinsics which have a close correspondence to the CPU instruction set, leading to significant speedups (at some cost in effort). Indeed, for optimal performance, many molecular dynamics codes such as GROMACS natively ship some explicitly vectorised hand written SIMD code for critical operations. Numpy also uses a similar strategy across a broader domain (see here).
How fast is distopia?
For calculating distances under periodic boundary conditions, distopia is between 5-15 times faster than the MDAnalysis compiled backend when measured at the C++ level, depending on the periodic boundary conditions, problem size and precision (float vs double) used. See Fig. 1 for a comparison including orthorhombic and triclinic periodic boundary conditions on my computer (which has an AMD Ryzen 9 7950X CPU).
Fig 1:
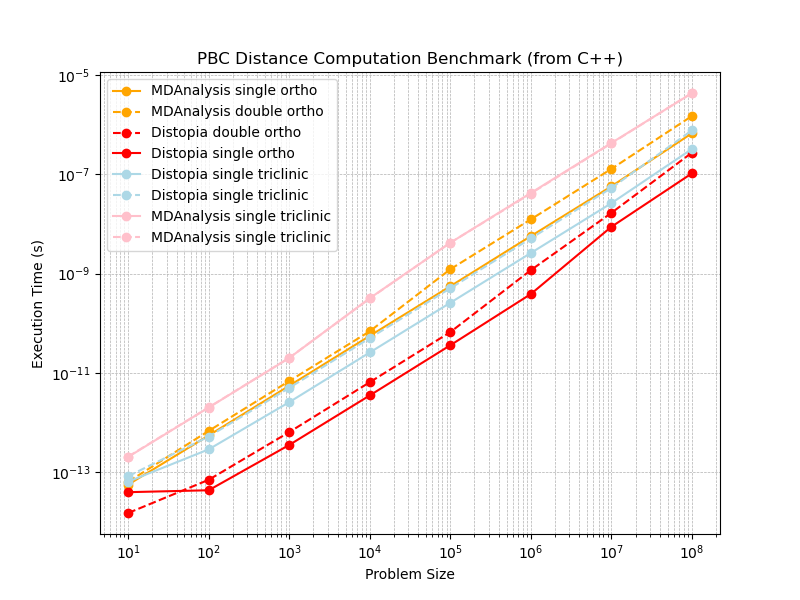
A large performance gain for distopia relative to the MDAnalysis C++ backend is observed. However could this be a poor baseline from the MDAnalysis backend rather than fantastic performance from distopia? Lets also test at the Python level relative to MDAnalysis, a naive implementation in Numpy and a JIT compiled version using JAX to see performance at the Python level (single precision) see Fig. 2.
Fig 2:
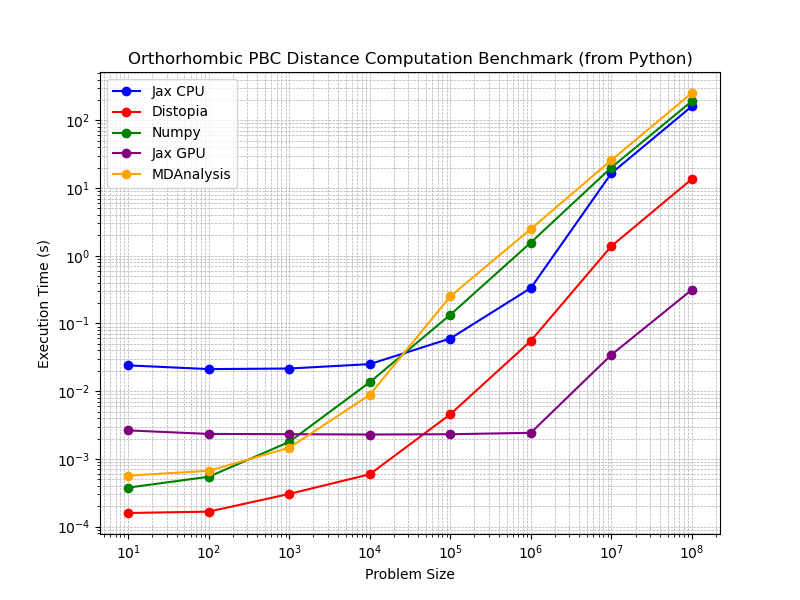
Indeed we see that distopia is significantly faster (often over 10x) than MDAnalysis, Numpy and JIT compilation with JAX (CPU). You can reproduce the plots in this Fig. 2 using code here: https://github.com/hmacdope/benchmark_distopia. Comparison with GPU enabled JAX is also included, which does show increased performance, however this is comparing a single thread to the whole streaming multiprocessor of my NVIDIA 4090, which is hardly a fair comparison (further discussions of GPUs below).
Similar speed improvements for distopia relative to other methods holds for angles and dihedral computations across the C++ and Python layers, but are omitted for brevity here. Distopia also ships with a set of inbuilt microbenchmarks (using googlebench) that can be used to easily determine and compare performance on your system.
Using distopia
You can install the latest version of distopia from conda-forge:
mamba install -c conda-forge distopia
You can easily use distopia as a standalone package to calculate distances (pairwise or outer product), angles and dihedral.
import distopia
import numpy as np
N = 10000
box = 10
# make random coordinates that overhang the box
c0 = np.random.rand(N, 3).astype(np.float32)*2*box
c1 = np.random.rand(N, 3).astype(np.float32)*2*box
box = np.asarray([box, box, box], dtype=np.float32)
# pairwise distances orthorhombic box
distances = distopia.distances_ortho(c0, c1, box)
# full distance matrix
distance_matrix = distopia.distance_array_ortho(c0, c1, box)
# pairwise angles in a general triclinc box just for fun
c2 = np.random.rand(N, 3).astype(np.float32)*2*box
triclinic_box = np.asarray([[10, 0, 0], [1, 10, 0], [1, 0, 10]], dtype=np.float32)
angles = distopia.angles_triclinic(c0, c1, c2, triclinic_box)
You can also use distopia as a backend for distances in MDAnalysis
import MDAnalysis
u = MDAnalysis.Universe("topology.pdb", "trajectory.xtc")
protein = u.select_atoms("protein and not name H*")
lipids = u.select_atoms("resname POPC CHOL and not name H*")
distance_array = MDAnalysis.lib.distances.distance_array(protein, lipids,
box=u.dimensions,
backend="distopia")
Note that use from MDAnalysis will not show the full performance gains available from the standalone package due to shims around precision needed for MDAnalysis distance API compliance. This is being actively worked on for MDAnalysis 3.0 (see issue here), however distopia is still regularly several times faster than the native serial distance backend.
How does distopia work?
To give a bit more technical detail on the design of distopia, we make extensive use of the cross platform SIMD capabilities of Google’s Highway library, with built in support for X86 and ARM SIMD of all widths, including modern 512-bit registers. Huge shoutout to the folks at Google for this awesome piece of technology.
Dynamic dispatch means that the optimal native implementation for your architecture is selected at run time, ensuring cross platform compatibility. We use a SIMD enabled conversion from Array Of Structs (AOS) to Struct of Arrays (SOA) layout (explanatory article) to use large-width SIMD at critical steps, enabling better register saturation than can be achieved in a AOS layout. This kind of large scale memory layout transformation is normally far outside the scope of an auto-vectorising compiler.
Why focus on CPU performance rather than use accelerators?
Why not use accelerators I hear you say? For large-scale molecular dynamics simulations, GPUs and other accelerators often provide immense computational speedups over and above those achievable with CPUs and SIMD (see JAX GPU benchmark in Fig. 2). However, not all workloads are well-suited for offloading to specialized hardware. Small to medium-sized problems, such as trajectory post-processing, or custom analysis tasks, often suffer from kernel launch overhead, memory transfer overhead, and poor utilization on GPUs which cannot be amortised over further GPU processing steps (force calculation, PME, etc etc) as they are in a fully fledged molecular dynamics code. Accelerators are also often expensive to use in general and provide poor value for money if underutilised. In short I believe there is still a lot of untapped potential in CPUs for everyday use.
Get in touch!
If you want to calculate distances, angles, or dihedrals under periodic boundary conditions, we would love you to try out distopia! We are also looking to make further improvements and would value any suggestions or feedback. Feel free to get in touch personally or on the issue tracker.